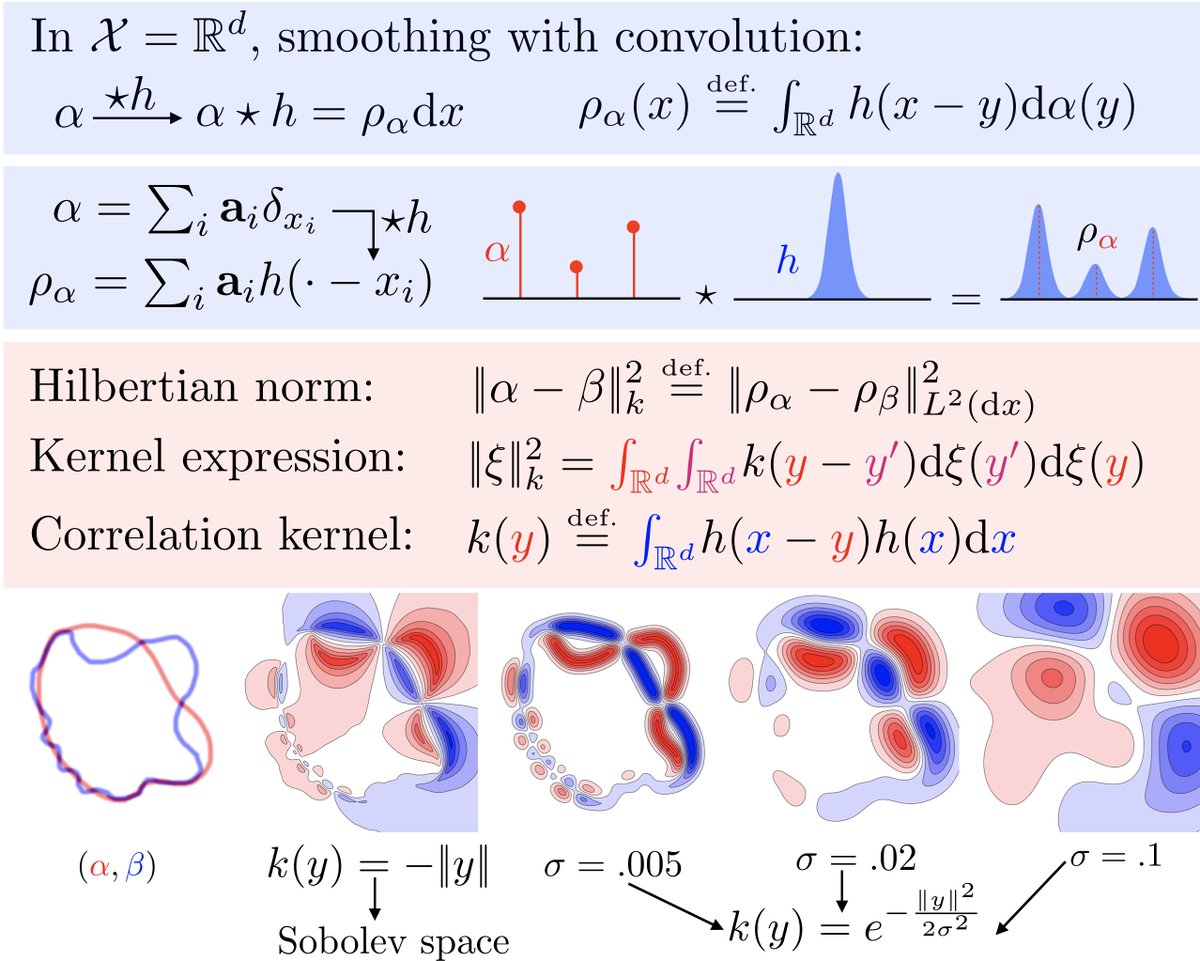
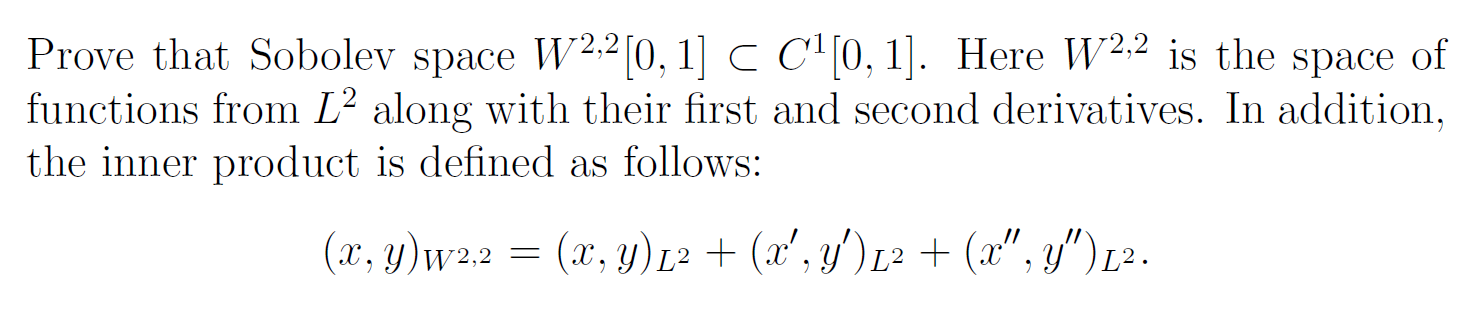Sobolev Space
Sobolev Spaces For Planar Domains Wikipedia
Solved Prove That Sobolev Space W2 2 0 1 C C1 0 1 He
Pdf Sobolev Spaces And Partial Differential Equations Imanol
Optimal Quadrature Formulas With Polynomial Weight In Sobolev
Gabriel Peyre On Twitter On Euclidean Space Maximum Mean
Sobolev Space An Overview Sciencedirect Topics
Pdf A New Characterization Of Sobolev Spaces On Mathbb R N
Das konzept wurde durch die systematische theorie der variationsrechnung zu anfang des 20.
Sobolev space. It is necessary to introduce the notion of weak derivatives and to work in the so called sobolev spaces. For p we set kuk kuka ess sup xa ux. Sobolev spaces adams robert a fournier john j. 9780120441433 kostenloser versand fuer alle buecher mit versand und verkauf duch amazon.
The space w p l w was defined and first applied in the theory of boundary value problems of mathematical physics by sl. Sobolev spaces introduction in many problems of mathematical physics and variational calculus it is not sucient to deal with the classical solutions of dierential equations. Notes on sobolev spaces peter lindqvist norwegian university of science and technology 1 lp spaces 11 inequalities for any measurable function u. Since its definition involves generalized derivatives rather than ordinary ones it is complete that is it is a banach space.
Spaces of weakly dierentiable functions so called sobolev spaces play an important role in modern analysis. The essential supremum is the. Ein sobolev raum auch sobolew raum nach sergei lwowitsch sobolew bei einer transliteration und in englischer transkription sobolev ist in der mathematik ein funktionenraum von schwach differenzierbaren funktionen der zugleich ein banachraum ist. The derivatives are understood in a suitable weak sense to make the space complete ie.
Products in sobolev spaces ethanyjae inthisnoteweprovethefollowingtwotheoremsaboutmultiplicationinsobolevspaces. A banach spaceintuitively a sobolev space is a space of functions possessing sufficiently many derivatives for some. Suppose s 1s 2 s and s 1 s 2 s. In mathematics a sobolev space is a vector space of functions equipped with a norm that is a combination of l p norms of the function together with its derivatives up to a given order.
